After several months at work using DX12 I got the itch for doing some low-level graphics work in my personal time, so I started my foray into Vulkan a few weeks ago.
I didn’t really want to start from some beginner’s tutorial so I did some hunting and found Arsen’s Vulkan streams which are perfect for what I wanted.
He blazes through the code explaining a lot of things, but with my DX12 experience, they’re quite brilliant because they get straight to the point and then I do my own digging into the spec.
This is the first time I’ve ever watched a coding stream and I’m really enjoying it. In my first ever development job in Malta, we did a lot of paired programming and this was ridiculuously useful. Seeing someone with 10+ years of experience coding (20+ in his case), making decisions and thinking out loud is very educational. One of the things that I like to hear the most about is not what they know about a topic but they learnt it - and seeing his problem solving approach is great.
Before I started it, I didn’t really have any major reason for leaning towards Vulkan other than curiousity, but at this point I’m pretty hooked, because of…
Validation Layers
The validation layers are tremendously helpful at telling you what might go wrong if you incorrectly setup certain structs. At some point I got a validation layer error that I wasn’t understanding, so I ran the debugger through the validation layer itself to see what was triggering it. Being able to see inside them was brilliant and a huge leap from the opacity that comes with DX12, albeit DX12 has a fantastic debug layer.
Mesh Shaders
Another major reason I was attracted to the streams was Mesh Shaders. They were a major reason for why I got my own RTX card, and having just finished the video where we get to do the mesh shading optimizations, I’m really looking forward to investigating more advanced uses for them. I’ve been fascinated with GPUs for a long time and I want to push my RTX to its limit with the amount of geometry it can process. Using the mesh shaders for doing extensive advanced culling is something I will definetly need when I try to process some of the massive scenes I intend to experiment with. The end goal is the Moana data set, we’ll see how that fares, I’m going to need a big GPU for that!
The main drawback is the lack of tools for debugging mesh shaders but more on that in the next section.
I’ll move the meshlet computation offline once I start working with bigger meshes because it can get quite expensive.
It seems Vulkan is still not as well-catered as DX12 when it comes to debugging and profiling tools. I’ve had a lot of NSight crashes and it’s the only decent free GPU profiling tool I can find. RenderDoc is robust but of no help when it comes to mesh shading. I’m quite disappointed with the debugging and profiling tools for Vulkan so far.
It seems DX12 has Mesh Shader debugging support in NSight but not Vulkan. With DX12 we used Pix extensively and it is loaded with a ton of useful features like performance counters, BVH visualization, gpu buffer readouts. NSight crashed immediately when I ran my Vulkan program :( I’ll have to check my driver compatibility, hopefully it’s something as trivial as that.
volk
Extensions are an integral part of Vulkan, and volk comes a long way in solving that problem. It’s useful but I did the mistake of not reading the fine print in the documentation. I was including it into my own project, but I did not replace the vulkan.h include with volk.h inside the libraries I was including in my own source, which resulted in me chasing a missing symbol related bug which appeared as a simple access violation. This swamped a whole Saturday and Sunday, resulting in a cancelled pub session and some time with Dark Souls. Learnt my lesson now!
# Vulkan Spec
The spec is super-detailed and well written but whoever thought that it should be in 1 web page deserves a world of pain! If it wasn’t in 1 page I would consider it to being one of the finest pieces of literature, comparable to PBRT and Lord of the Rings :)
Reading the spec is very valuable, a lot of nuances are explained. The DX12 spec wasn’t this detailed (although it’s improved and I believe they’ve now released some really detailed documentation on GitHub).
Verbosity
Brace yourself for a lot of typing. In terms of verbosity it seems to go OpenGL -> DX11 ———–> DX 12 —> Vulkan. You have to write a lot of code to get things up and running. My previous experience with DX 12 prepared me for this so it was no shocker, but it can get exhausting.
Predictability
Using the Vulkan C API becomes very intuitive once you get used to the nomenclature. The validation layer guides you when you do something wrong, the structs follow a similar structure and so you kind of get used to the verbosity.
Final Thoughts
If you’ve never tried a low level graphics API, give Vulkan a go. It’s been a great experience (sometimes aggravating but what’s the fun in graphics programming if you sometimes don’t want to scream) and learning how the GPU works is something every programmer should do.
I’m loading the Buddha obj and rendering it using a mesh shader pipeline, returning the surface normal as a colour in the fragment shader. I’m using ImGui to display some stats, such as the FPS, GPU time and a plot of the GPU time. I store 100 samples and plot them, using the min and max of the samples to get it displaying well, otherwise it’s pretty much a straight light since the computation time doesn’t fluctuate much.
I’d be lying if I told you that you should look at my code, but you shouldn’t. It’s a horrible mess that’s been written in haste and hacky. But there is hope: I’ve also been watching Yan Chernikov’s Game Engine series which is reaaaallllllyyyy good and once I do a forward pass and a deferred pass in Vulkan, I’ll re-start the whole process and write th engine in a modular cleaner fashion. Unfortunately for now, all I have is a lot unclean code, but HEY IT WORKS SUE ME!
Here’s a pretty image of where I’m at:
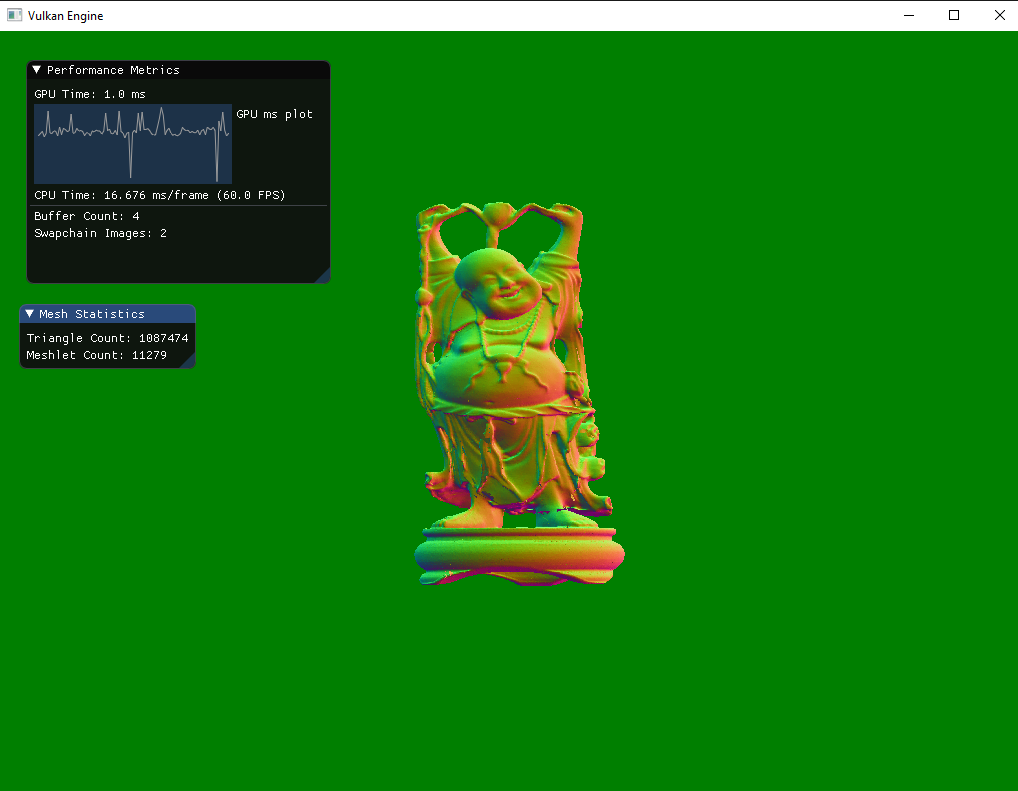
With that, I’m signing off. If you have any questions feel free to reach out to me on Twitter or LinkedIn or email, ciao!
Working on my renderer sometimes leads to some hair-tearing moments when bugs start to come up. When you’re tracing millions of rays and you’ve got millions of pixels, tracking down a visual bug is very tricky.
This blog post is the first in a series where I’ll discuss what I did to debug certain bugs that I encountered. The series isn’t planned - when I get a bug which gives me a lot of grief, I’ll write down what I did to find it and fix it.
I’ll preface that my renders look slightly darker than PBRT’s. I have many missing features such as RR, MIS, QMC sampling, all which affect this. I also have very basic sample filtering (just a box filter) and the renderer is not feature compatible with PBRT. Other than that though, it should look close enough to PBRT.
When I implemented my glass material and compared the rendered image to PBRT there was a huge difference between them:

This is the kind of bug that is quite difficult to debug - you have specific paths related to specific geometry which are misbehaving. Of course I knew where the problem, it’s somewhere in the Glass Material and Specular Transmission and Reflection BxDFs ( or so I initially thought :) ).
The first thing I started looking at was my Fresnel functions. Since that’s the function that determines whether a ray is refracting or reflecting, this made sense to me. I computed the function for certain angles and certain reflective indices by hand and wrote unit tests to confirm matches which they did.
With this out of the way, I looked at the refraction function and did the same - however everything was fine here too.
At this point I knew I needed to get in deeper, so I had to write some utlity code to be able to walk through a single pixel path, using the debugger and not render a full frame until I get to that pixel.
Coding it up didn’t require a lot of effort however working out what the ray was supposed to be doing required a lot of hand calculations. Another way to do this is to use an open source renderer and debug it, PBRT and Mitsuba are the 2 obvious suggestions.
Once I started up the renderer and had my first ray intersection with the glass, the ray was supposed to refract into the surface. The next bounce was going to be inside the glass and hit the other side of the box from the inside, and exit. My ray did no such thing! As soon as it was refracted inside the box, it refracted again but for some weird reason, it went back inside the box (which is actually a reflection). I had a hunch something was up with my normals, so I had a look through the code that might have been modifying the normals and realized that I was prematurely face forwarding my normals when I was populating my surface interaction record right after the first intersection.
I had not noticed this bug before because I was not transmitting rays through a medium for the Mirror and Matte material so it was never an issue.
Fixing that bug significantly improved my image


but this was completely different! I realized that having modified the normals during the surface interaction record population, another place where I was faceforwarding normals liberally was my Next Event Estimation code. I cleaned up this part of the code, rendered, got a match with PBRT and introduced reflection back in:

At this point I introducted the reflection back in but had a bug. I had been going at this for quite a few days (over a week), with only an hour or 2 to spare after work to look at this bug. So I took a bit of a shortcut and debugged a single ray through PBRT. This one I found with PBRT very quickly - I wasn’t setting the SpecularBounce flag to true when I was reflecting from a dielectric and so was computing direct lighting on a specular reflective surface. Fixing that gave me the final image:

Which is pretty much what PBRT is getting albeit slightly darker.
One of the major pieces of advice I can give to people who are about to start their foray into ray tracing is the importance of unit testing. Testing every little function properly means that all the small moving parts work and gives you some peace of mind when using them and you’re hunting for a bug you might have.
I’m dedicating my August to just writing unit tests for my existing code - I was doing that for some stuff but in my haste to get some features up and running, I neglected that part and it bit me in the ass finally :) Having said that, I do look at bugs as a potential learning experience, and this kind of bug allowed me to gain a more solid understanding of surface reflection.
Another thing that was informative was following a path in PBRT. With a tool like the Visual Studio Debugger, this becomes quite easy.
One thing which I really want to do is render a single path, and in the mean time have my Vulkan engine draw the path and the normal of each surface intersection, and hovering over the intersection point, I can get the material details, the fresnel reflectance value if it was a specular surface, that kind of stuff. I have given it a lot of thought and would love to do this but time is a major obstacle.
That’s all I have today on this! The next post will probably be on debugging acceleration structures, the only issue is that I did the coding working on acceleration structures around February and as a result, my memory is a little hazy on my efforts so I might end up writing another acceleration structure to jog my memory and get new bugs, solve these problems and share the “wisdom”, with that, ciao!